Tracés de base des jardins

Pour votre jardin, vous avez simplement besoin d'un cordeau et de quelques piquets pour implanter un potager, des allées, un bassin ou tout autre élément de votre petit paradis. Sur le papier, une règle et un compas remplaceront le cordeau et les piquets.

Cercle et arc de cercle

Avec un piquet et une corde ou avec un compas

Au jardin:

1. Plantez un piquet au centre du cercle.
2. Attachez la corde au piquet
3. Donnez-lui la longeur de rayon désiré et faitez le tour avec la corde tendue en marquant le cercle soit avec un piquet si la terre est nue soit avec du plâtre si c'est du gazon.

Sur le papier:

1. Ajustez votre compas à la longueur de rayon désiré.
2. Plantez la pointe au centre du cercle.
3. Faites-le tourner pour tracer le cercle

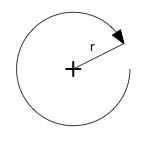
Pour un cercle complet on fait tout le tour. Pour un arc de cercle on s'arrête en chemin. L'arc de cercle est la base essentielle pour toutes les implantations au jardin.

Comment trouver le centre d'un cercle inscrit entre 3 murs ? regardez la figure du cercle inscrit dans le triangle ci-dessous. Elle montre comment tracer les deux bisectrices en pliant la corde des arcs de cercle en deux.

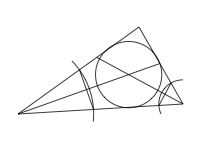
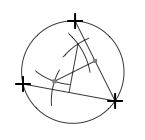
Pour tracer le cercle inscrit entre trois points regardez d'abord comment tracer une droite perpendiculaire au centre d'un segment.

Faire une courbe avec des arcs de cercle bien raccordés

Pour avoir des lignes fluides et une implantation simple sur le terrain

Deux arcs de cercles se raccordent si leurs rayons sont sur la même droite.

Tracer une droite perpendiculaire et centre d'un segment

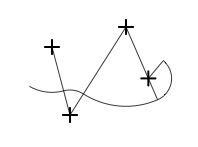
Les perpendiculaires sont très utilisées dans les jardins

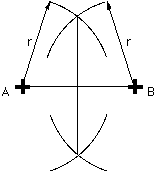
Le rayon utilisé (r) n'a pas beaucoup d'importance. On est pas obligé de tracer des deux côtés de la ligne AB. Le milieu du segment est facilement obtenu en pliant la corde en deux. Si on veut une perpendiculaire au centre de la porte d'entrée d'une maison non placera les deux points A et B à égale distance de chaque côté de la porte.

Angle droit

Avec deux rubans à mesurer ou une corde à 13 noeuds (12 intervales)

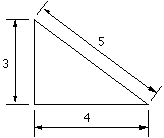
Les proportions 3, 4, 5 des côtés produisent un triangle rectangle. Attention on ne peut pas prendre n'importe quel chiffre. En revanche on peut prendre n'importe quelle unité de mesure de longueur, des mètres des pieds ou des intervales de longueur identiques dans une corde.

Avec deux rubans à mesurer:

1. Mesurer le segment de 3 mètres. Plantez deux piquets.
2. Tenez dans chaque main un ruban à mesurer. L'un fixé à 4 mètres et l'autre à 5 mètres.
3. Formez le triangle. Plantez le troisième piquet.

Avec une corde à 13 noeuds

1. Placer deux piquets à 3 noeuds de distance
2. Tenez les deux extrèmités dans la main et faites passer la corde autour des deux piquets.
3. Reculez jusqu'à ce qu'il y ait 4 noeuds d'un côté et cinq de l'autre. Plantez le troisième piquet.

Avec un compas et une règle:

1. Tracez un segment de droite de 3 unités.
2. À l'une des extrémités tracez un arc de cercle de 4 unités et à l'autre un arc de cercle de 5 unités.
3. Tracez les deux côtés avec la règle.

Tracer deux parallèles

Indispensable pour les sentiers

Deux droites parallèles. Utiliser le triangle 3-4-5 deux fois. L'unité de mesure sera un tiers de la distance entre les deux droites. En enroulant une corde 4 fois entre les deux points de départ on fabriquera facilement une corde à treize noeuds parfaite pour ce tracé.

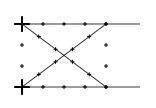
Deux arcs de cercle parallèles. Utiliser le même centre et allonger le rayon.

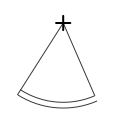
À partir d'une forme incertaine, utiliser un bâton (un ruban à mesurer) et tenez le perpendiculairement à la courbe. Mais si vous tracez vos courbes avec des arcs de cercle bien raccordés vous n'aurez qu'à utiliser les mêmes centres.

Polygones inscrits dans un cercle

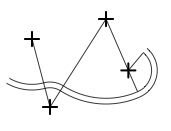
À la base des tracés de parterres de fleurs et des compositions plus importantes

Le tracé des polygones est approximatif mais peut facilement être tracé sur le terrain avec un cordeau et des piquets et sur papier avec un compas.

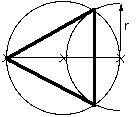
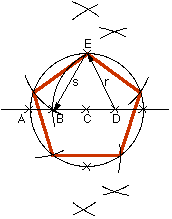
Triangle: Le rayon r est celui du cercle
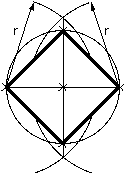
Carré: Les deux rayons r sont identiques et indépendante du cercle
Pentagone: Sur le cercle de centre C et de rayon AC placez E tel que EC soit perpendiculaire à AC puis D tel que CD soit égal au demi-rayon du cercle. Utilisez le rayon r de centre D passant par E pour déterminer le point B sur le diamètre du cercle. Le rayon s reporté sur le cercle permet de tracer le pentagone.
Hexagone: Utilisez le schéma du triangle et reportez le rayon sur le cercle à partir des sommets du triangle.
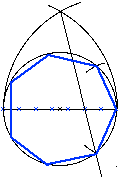
Pour faire un polygone avec un nombre n de côté (avec approximation suffisante en jardins), on divise le diamètre en n parties. On place le point d'intersection des deux arcs de cercle ayant un rayon équivalent au diamètre du cercle. On fait passer une droite par ce point et par le deuxième point de division du diamètre. L'intersection avec le cercle donne le côté du polygone.

Tracer une ellipse

Deformer un cercle pour jouer avec la perspective est fréquent dans les jardins

La distance cumulée aux deux foyers de chaque point du contour de l'ellipse (AC+CB) est constante et égale à son grand axe (2r).

Au cordeau

1. Tracer le grand axe et le petit axe
2. Placer les deux foyers en traçant des arcs de cercles (rayon égal à la moitié du grand axe) à partir des extrémités du petit axe
3. Prendre une corde de la longueur du grand axe fxée aux deux foyers A et B
4. Tracer le contour avec un piquet (c) qui glisse à l'intérieur de la corde

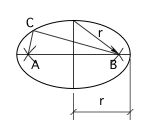
Pour éviter de changer la corde de côté quand on arrive dans l'extrémité du grand axe, on peut utiliser une corde de deux fois la longueur du grand axe. On l'attache pour former un anneau. Le piquet C et les deux foyers A et B permettent alors de tendre un triangle qui va glisser facilement tout au long de l'éllipse sans interruption.

Ne confondez pas l'ellipse et l'ovale. L'ovale est contruit avec deux cercles égaux et deux arcs de cercle de rayon égal au diamètre des cercles. Dans sa proportion classique les deux cercles sont placés à une distance d'un rayon pour partager en trois le grand axe. Pour tracer l'ove, on fait un cercle, puis le côté de l'ove avec un arc de cercle égal au diamètre qu'on arrête quand il coupe le côté du cercle qui est le centre du petit arc de cercle.

Spirale

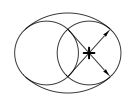
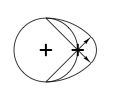
Simple à tracer

Commencer par placer les 3, 4 ou 6 piquets au centre et enrouler la corde en sens inverse de la spirale. Dérouler pour tracer la spirale.

Remplissage du plan

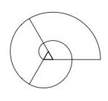
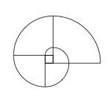
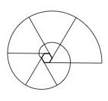
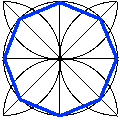
Pour les pavages et les plantations, on crée le plus souvent une matrice de remplissage

Le triangle et le carré permettent un remplissage régulier par un seul motif, mais pas le pentagone cf Penrose.

Pour approcher le pentagone avec un remplissage régulier on opère un remplissage en quinconce. Le quinconce est un remplissage carré avec décalage d'une rangée sur deux de la moitié du côté du carré.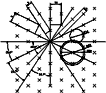

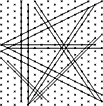
Voir les différents remplissages du plan par les plantations.

Couper un segment en parties égales à partir d'un autre tracé parallèle

C'est plus facile de multiplier une longueur que de la diviser.

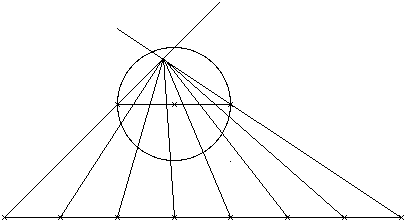
La première droite est obtenue par addition de parties identiques. Le point de convergence est obtenu par liaison des extrémités des deux segments parallèles. Pour diviser un segment en 3 5 7 11 ou tout autre nombre il suffit d'additionner autant de parties sur la ligne parallèle.